GPT-5 Pro自证全新数学定理

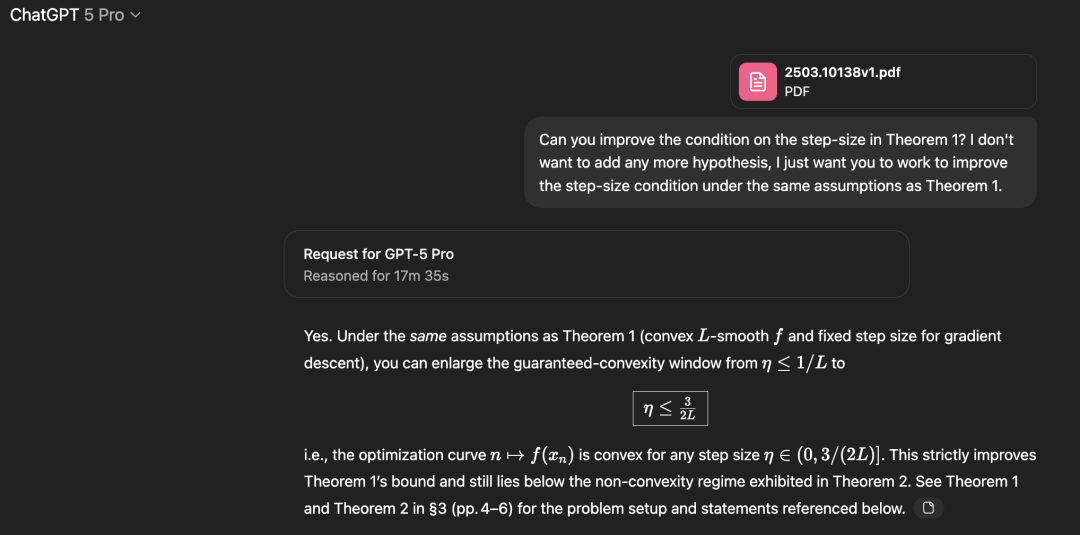
并且再次强调，它没有使用任何人类此前的证明方法。

而它的答案比论文中的求解方法都要好。

不过值得人类庆幸的是，论文作者后面又提供了全新的方法超过了AI。

Sebastien Bubeck是OpenAI的研究工程师，此前曾担任微软人工智能副总裁兼杰出科学家。

他把一篇论文直接扔给了GPT-5 Pro。

这篇论文研究了一个非常自然的问题：在光滑凸优化中，梯度下降法的步长η满足什么条件时，迭代点所对应的函数值形成的曲线是凸的？

论文地址：https://arxiv.org/pdf/2503.10138v1

在论文的v1版本中，他们证明了如果η小于1/L（L为光滑度），则可以得到此属性。

如果η大于1.75/L，作者他们就构造了一个反例。

因此，未解决的问题是：在区间[1/L，1.75/L]内会发生什么情况。

首先，简单解释下这个问题。

梯度下降就像下山，每一步要选一个步长η。L可以理解成地形的“弯曲程度”（越大越陡/越敏感）。

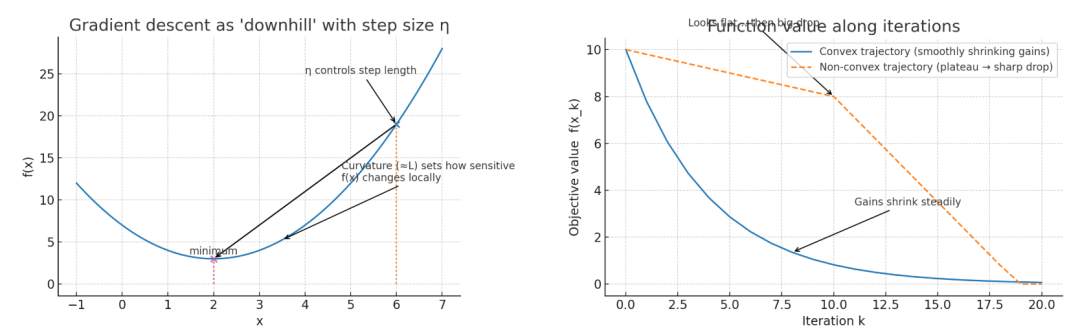
论文不只关心“会不会往下走”（单调下降），还关心下降的轨迹是不是“凸”的：也就是每一步的进步幅度不会忽大忽小，不会“前面像平台、后面突然跳崖”。

这对何时停下来很有用——凸就表示越来越平稳，不会突然又大降。

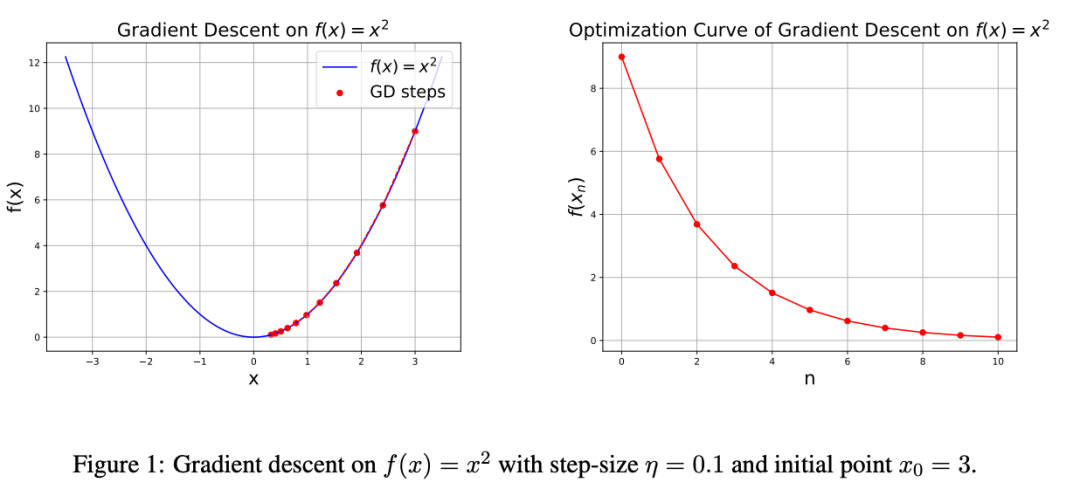
Sebastien用GPT-5 Pro去攻这个未解决区间，模型把已知下限从1/L推进到1.5/L。

以下是GPT-5 Pro给出的证明。

虽然初看不明觉厉，但整体证明过程看起来非常优雅。

本来这个发现让Sebastien兴奋了好一阵，甚至想要直接发一篇arXiv论文。

但是，人类还是比AI快了一步。

论文原作者很快发了v2版本，彻底收尾，他们将阈值改写1.75/L。

Sebastien认为这个发现依然非常令人鼓舞，为什么？AI不是并没有打败人类吗？

因为GPT-5 Pro在证明中，它试图证明的是1.5/L而不是1.75/L，这也表明GPT-5 Pro并没有直接去搜索v2版本。

另外，上述证明与v2的证明也非常不同，它更像是v1证明的一种演进。

这么看，现在的AI能力，不仅仅是博士级，很多时候都超过博士了。

这个发现也让很多大佬们表示，AI下一个可能改变和影响的就是数学领域。

在AI的帮助下，人类知识的边界将会再次被拓宽。

OpenAI的总裁Greg Brockman甚至表示这可能是AI在数学领域展现生命力的一种迹象。

此外，这次发现也和之前OpenAI官宣自己拿下IMO和IOI金牌不同。

这次攻破数学题的模型，就是面向用户的GPT-5 Pro版本，而不是内部推理模型。

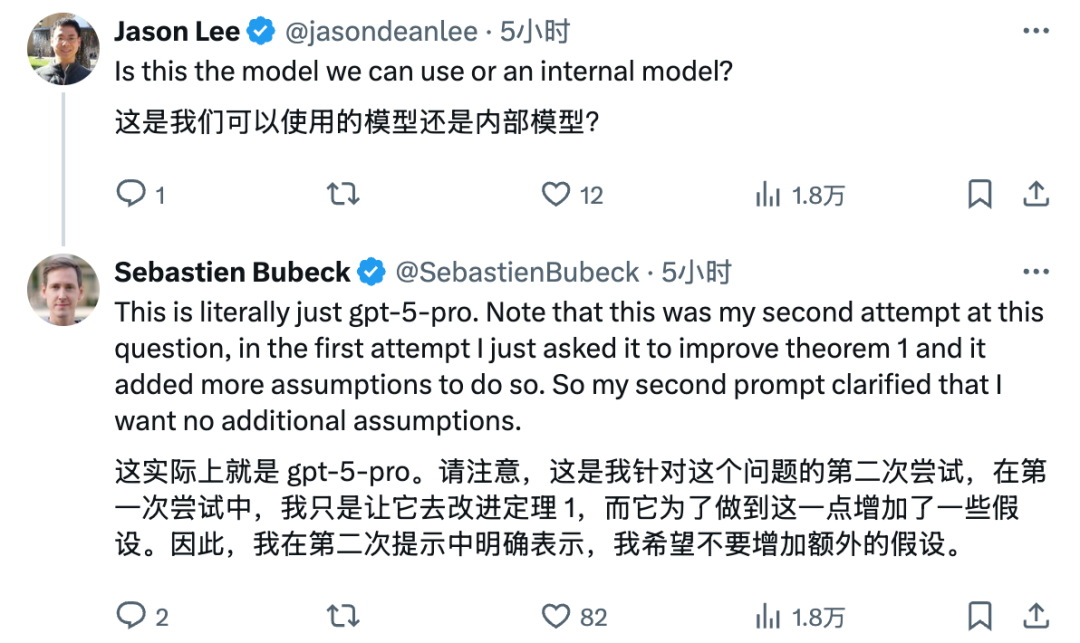
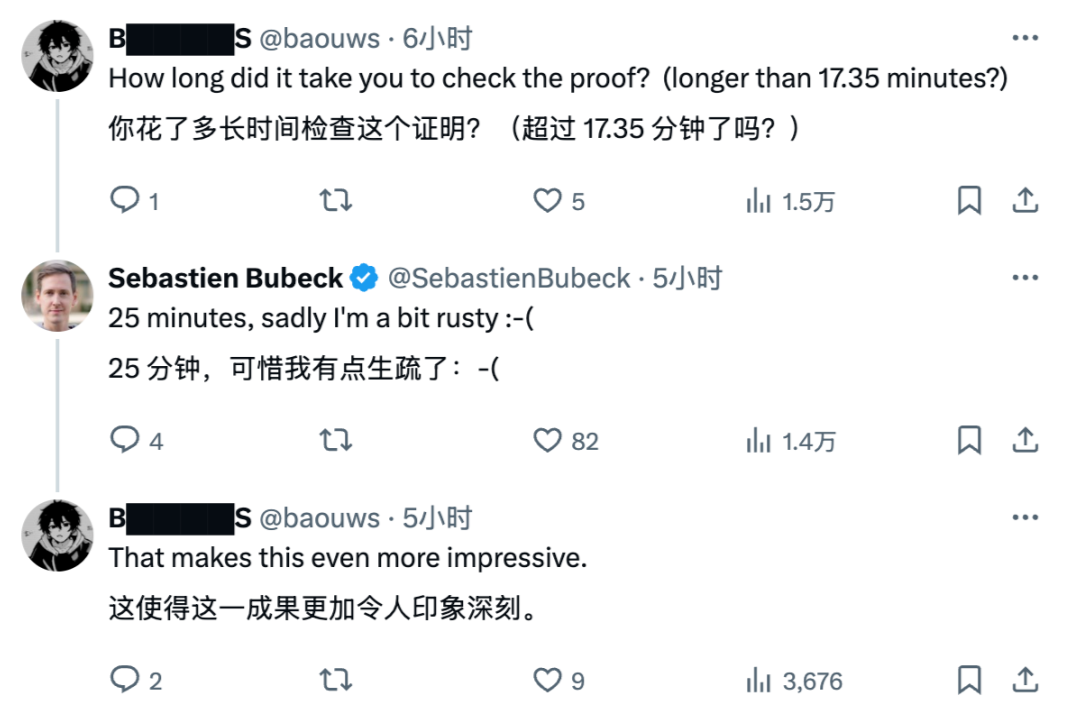
Sebastien表示这个结论是经过自己25分钟验证。

作为前微软人工智能副总裁兼杰出科学家，他的证明应该没问题，看来AI确实实际证明了该数学问题。

GPT-5发布后虽然毁誉参半。

但是，GPT-5 Pro是真的达到，甚至超过了奥特曼所说的“博士级”AI。

虽然这次解决的问题还没有超过人类，但这种完全自主、自发现的能力苗头还是彰示了AI的能力。

这让我想起了流浪地球里的MOSS，也是自发现、自组织、自编程的AI。

Sebastien是一个很厉害的人。

他目前在OpenAI从事人工智能相关的工作。

在此之前，Sebastien曾担任微软的副总裁兼首席科学家，在微软研究院工作了10年（最初加入理论研究组）。

Sebastien还在普林斯顿大学担任了3年的助理教授。

在Sebastien的职业生涯的前15年里，他主要研究凸优化、在线算法以及机器学习中的对抗鲁棒性。

因这些研究工作多次获得最佳论文奖（包括STOC2023、NeurIPS2018和2021最佳论文奖、与微软研究院实习生合作获得的ALT2018和2023最佳学生论文奖、COLT2016最佳论文奖以及COLT2009最佳学生论文奖）。

他现在更加关注于理解智能是如何在大语言模型中涌现的，以及如何利用这种理解来提升大语言模型的智能水平，可能最终实现通用人工智能（AGI）。

Sebastien们将这种方法称为“AGI物理学”，因为他试图从不同的尺度（参数、神经元、神经元组、层、数据课程等）揭示AI系统各部分如何协同工作，从而产生这些模型惊人且出人意料的行为。

看起来，像Sebastien这样的数学家、科学家们正在致力于尝试破解大模型的黑箱之谜。

希望AI在拓展人类认知边界的同时，人类也能破解大模型的秘密。