自由大学柏林的数学家在最新研究中指出,平面镶嵌(tessellation)远不只是视觉上的装饰艺术,其背后隐藏着解决复杂数学问题的有力工具。 所谓镶嵌,是指用几何图形在平面上无缝铺满、既不重叠也不留空隙的图案,研究团队证明,这类结构不仅具有强烈的审美吸引力,同时还能作为分析复杂方程和边值问题的数学框架。

这项由海因里希·贝格尔(Heinrich Begehr)与王大江(Dajiang Wang)合作完成的研究,发表在期刊《Applicable Analysis》上,结合了复分析、偏微分方程和几何函数论等多个领域的思想。 研究聚焦于所谓“镶嵌—反射原理”(parqueting-reflection principle):通过沿多边形边界不断做几何反射,将一个局部图形扩展为铺满整块平面的规则图案。
这种方法与大众熟悉的埃舍尔(M.C. Escher)式艺术镶嵌有相似之处,但研究表明,它在数学上的价值远超视觉效果。 具体而言,该原理为处理经典边值问题(如在数学物理中经常出现的狄利克雷问题和诺伊曼问题)提供了一种系统方法,使得在镶嵌区域内部构造函数表示成为可能。
贝格尔表示,数学之“美”不仅是一种审美判断,更体现为结构上的深度与计算上的高效。 与此前主要关注“能否铺满平面”的镶嵌研究不同,利用镶嵌—反射原理生成新的镶嵌图案,可以直接转化为具体的函数表示工具,在数学物理和工程等领域具有潜在应用价值。
研究的一个重要成果,是能够给出格林核(Green kernel)、诺伊曼核(Neumann kernel)以及施瓦茨核(Schwarz kernel)等“核函数”的显式公式。 这些核函数在解决各类边值问题中居于核心地位,新的构造方法由此在几何直观与严谨分析之间搭建起清晰的桥梁。
过去十年间,“镶嵌—反射原理”在青年学者中持续引发兴趣。 自该概念提出以来,已在自由大学柏林催生了十五篇学位论文与结题论文,在德国以外的高校也推动了七篇博士论文的完成。
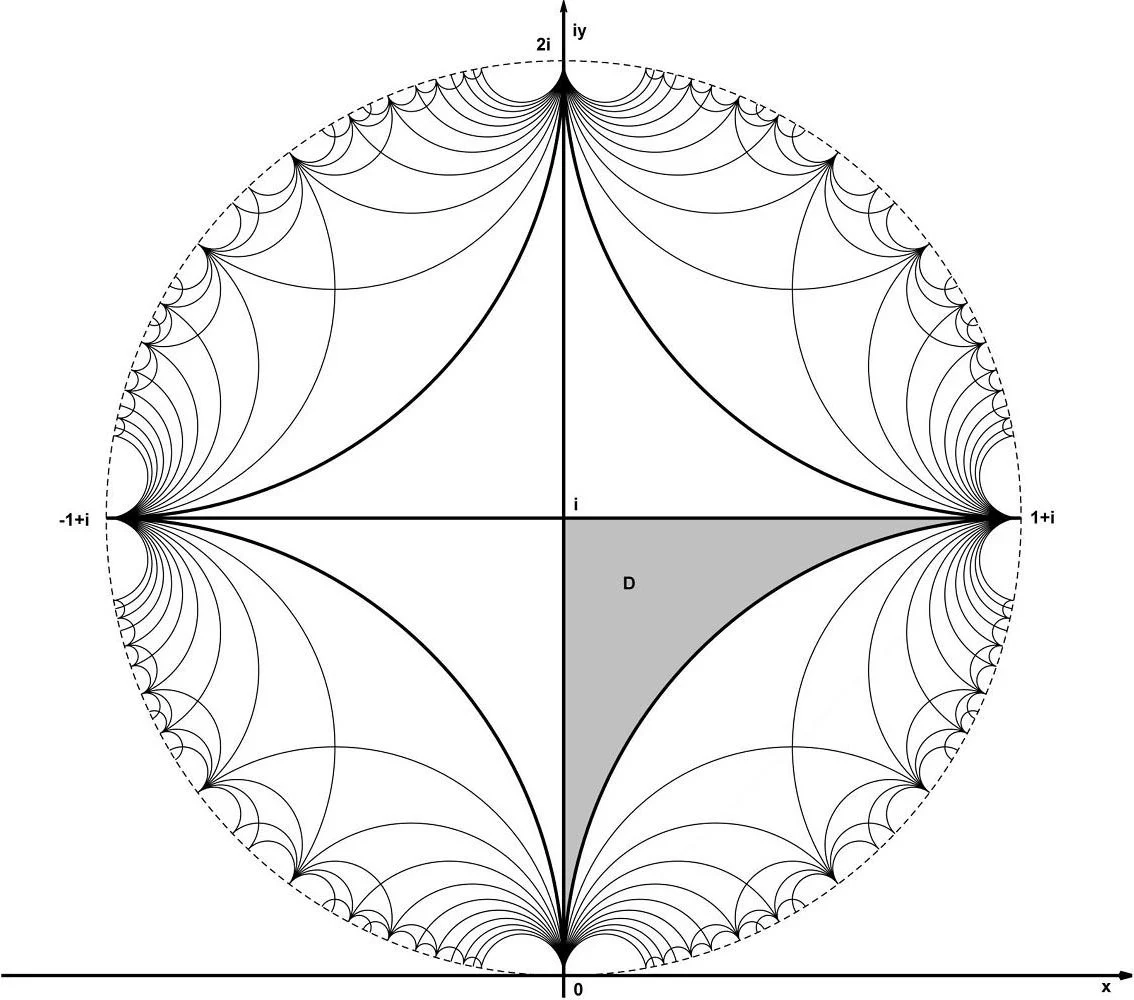
值得注意的是,这一原理并不局限于欧几里得空间,在与理论物理和时空可视化密切相关的双曲几何中同样适用。 2024 年,贝格尔在《Complex Variables and Elliptic Equations》上发表论文《Hyperbolic Tessellation: Harmonic Green Function for a Schweikart Triangle in Hyperbolic Geometry》,展示了如何在双曲平面上一块名为“施魏卡特三角形”(Schweikart triangle)的区域内构造调和格林函数。
王大江表示,希望这项工作不仅在纯数学和数学物理内部产生影响,也能为建筑设计和计算机图形学等领域带来新的灵感。 研究团队强调,当代图形软件和数字工具与这些数学构造结合时,可以进一步放大其视觉和应用潜力。
近二十年来,贝格尔在自由大学柏林数学研究所领导的团队一直致力于研究所谓“柏林镜面镶嵌”(Berlin mirror tilings)。 这一方法源自柏林数学家赫尔曼·阿曼德斯·施瓦茨(Hermann Amandus Schwarz,1843–1921)提出的统一反射原理:通过反复反射由直线与圆弧构成边界的“圆多边形”,最终得到覆盖整个平面的无缝镶嵌。
这些图案不仅视觉上极具冲击力,更重要的是,它们能够产生函数的显式积分表示,这是解决复杂边值问题的关键工具。 贝格尔形象地回顾说,早期数学家只能借助“三面梳妆镜”来制造无限反射的画面,如今则可以用迭代计算机程序生成同样效果,并辅以复分析中的精确公式。
在双曲空间中(例如单位圆盘内)的镶嵌,被认为在视觉上尤为惊艳,却也给数学处理带来特殊挑战。 施魏卡特三角形——一种具有一个直角及两个“零角”的特殊三角形、以业余数学家兼法学教授费迪南德·库尔特·施魏卡特(Ferdinand Kurt Schweikart,1780–1857)命名——正是在这种背景下成为焦点。
这类三角形可以在圆盘内形成规则、完整的镶嵌,其呈现出来的图案为计算机图形艺术家和建筑师提供了新鲜的审美素材。 与此同时,其背后的数学构造极为复杂,依赖高度发达的分析方法支撑。
研究团队指出,这些成果再次表明,数学不仅是一门抽象学科,还是一门高度“可视”的科学,结构、对称与美感在其中扮演核心角色。 在现代可视化技术、图形软件和数字工具的加持下,镶嵌与反射原理的应用前景有望进一步拓展,从理论探索延伸到工程实践与视觉创作等多个领域。
编译自/ScitechDaily

