
要知道,陶哲轩擅长的分析、数论、组合学等研究的往往是整数、函数、算子的性质。而微分几何更侧重于流形的性质,常用的工具也很不一样。
陶哲轩只是按自己直觉给了一个大致方向,GPT-5 Pro就从复杂计算到严谨证明一气呵成,帮助陶哲轩捕捉关键逻辑,突破传统思维局限。

甚至在AI帮助下最终发现自己的直觉有误,但通过这个过程更好理解了问题。
有了这次跨界解题的经验,陶哲轩对AI在学术研究上的作用也有了新的思考,他总结到:
AI在小尺度上很有用,中尺度上有些无益,大尺度上又有帮助。
AI从计算到证明一气呵成
先来看看原始问题,是3年前就在mathoverflow上提出的:
设一个三维空间中的光滑拓扑球面围成的区域,且曲面的主曲率绝对值不超过1,那么它包围的体积是否至少等于单位球的体积?

陶哲轩最初的思路是将问题限制在星形区域上,借助积分不等式推进。但他的微分几何有些生疏,所以请AI帮他进行这些计算。

结果GPT-5 Pro思考了11分18秒,不仅完成了所有计算,还直接给出了星形情况下问题的完整证明。
证明过程运用了各种不等式和恒等式,其中有些陶哲轩熟悉(比如Stokes定理和Willmore不等式),也有一个他也第一次接触的Minkowski第一积分公式。
有了这些不等式,加上算术-几何平均不等式,星形情况的证明实际上就是一行论证。
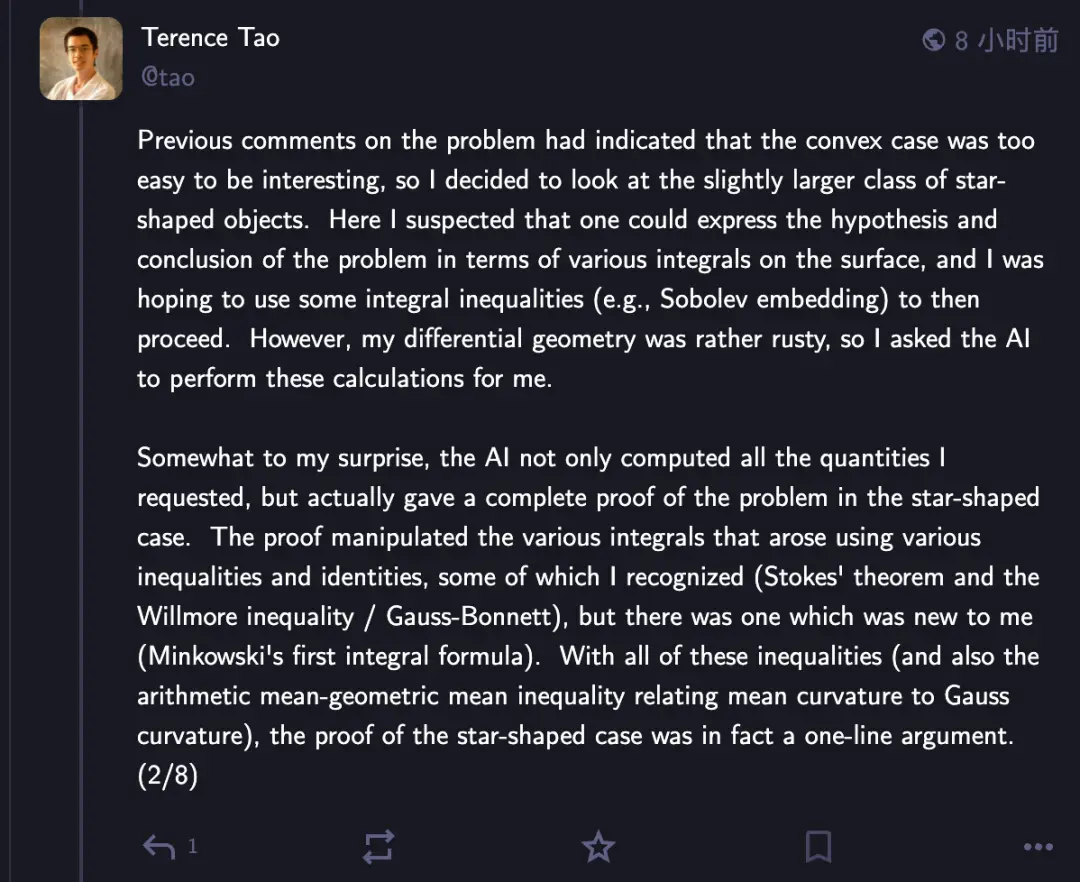
到目前为止,一切顺利。
接下来他需要验证证明的各个步骤,但网络上没有找到有用的资源。
再次询问AI后,直接得到两个令他满意的证明:一个是按照他建议使用散度定理的路线,另一个是基于他没想到的流方法。
通过AI的计算和证明,陶哲轩打算将其视为一个扰动椭圆偏微分方程问题,AI在这个思路上表现也良好。

虽然在估计一个扰动非线性项时出现了轻微的错误,但并非无法修复。而且AI还主动指出一个特殊情况其实又能回到星形的结果。
成功地用偏微分方程扰动理论的方法,解决了当曲面形状与单位球面差距不大(Small Data)时的情形。
但真正困难且未解决的,是当曲面形状与球面差距巨大(Large Data)时的问题。
陶哲轩意识到可以用将问题简化为一个大型有限计算,但AI用这个方法给出的结果非常混乱且缺乏启发性,本质上是对所有可能形状的穷举。
最终陶哲轩发现他设想的数值方法或许可以在有限的时间内解决所有给定条件的特殊情况,但无法处理一般情况,但AI只是按照提问照做了。

最后总结一下:虽然问题最终还是没有完全解决,但在AI的帮助下陶哲轩对这个问题的理解深入了很多。
陶哲轩的思考:AI工具的多尺度价值
虽然解题告一段落,但陶哲轩的思考还在继续。
回顾整个解题过程,AI在“小尺度”问题上表现得很好,只犯了一些小错误,并贡献了一些文献中已有的,但陶哲轩之前并不知道的有用想法。
但是要想进一步推进这个问题,就需要真正的微分几何专家的帮助了。

在“中等尺度”的策略上,AI略微显得无益,它强化了陶哲轩对问题的错误直觉,而不是提出质疑。
陶哲轩一开始的直觉是错的,AI也没有发现问题,基本上只是附和同意他说的一切。

但是在从获得对问题理解的“大尺度”指标来看,AI又是有帮助的,尽管主要是间接意义上的:在AI的帮助下能够更快地研究并最终放弃一种现在认为不适合的方法。

陶哲轩将这次经历与他之前的实验进行了对比。
在之前的实验中,他给AI一个他对结果有很好直觉的任务。这种情况下AI更有创造力,提供了他不知道的信息,但引导AI朝着富有成效的方向前进也明显更加困难。
他认为,在自己专业领域之外的问题上与AI互动似乎确实有一些价值,但必须谨慎行事并保持对情况的认知。

这次经历还印证了陶哲轩之前提出的观点:必须在多个尺度上衡量一个工具的有效性。
此前他提出了四个不同的效率衡量尺度:形式化证明中的任何单行、任何单个引理、任何定理的完整证明,以及整本教科书。
许多当前的自动化工具可以在其中一个尺度上加速形式化,但反直觉的是,过度依赖这样的工具可能最终会降低在其他尺度上形式化的能力。

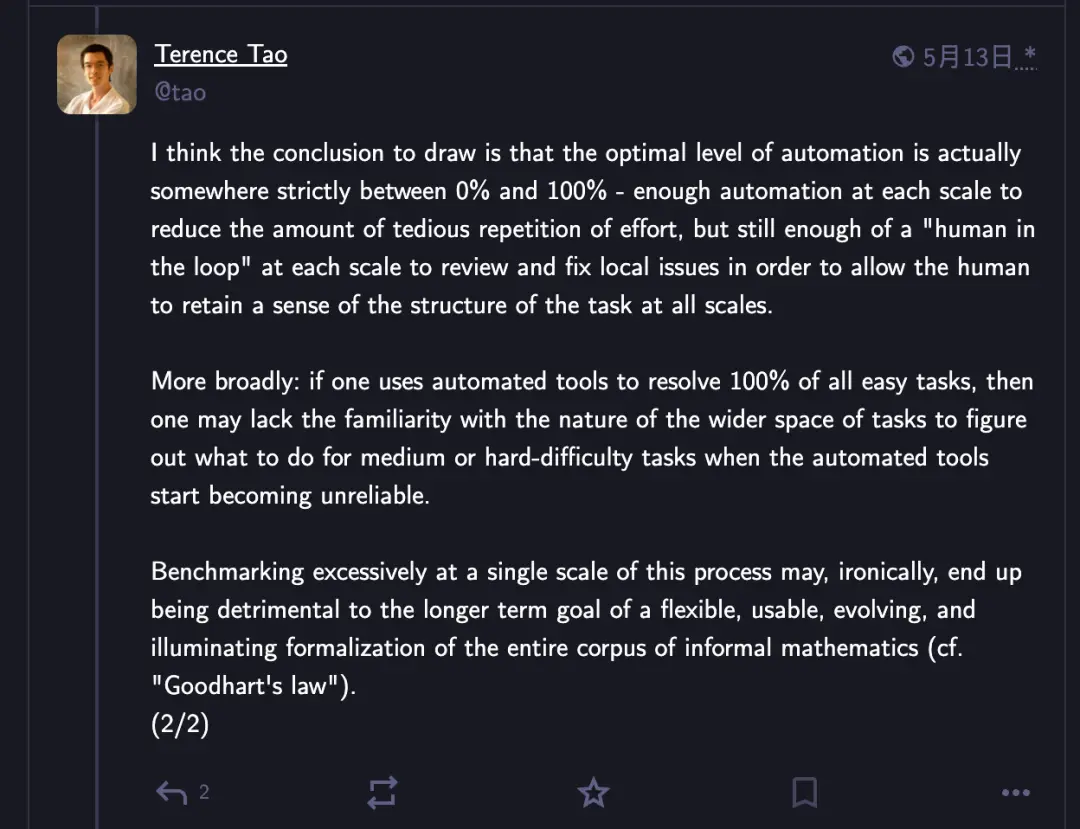
他认为最优的自动化水平实际上严格介于0%和100%之间。
在每个尺度上都有足够的自动化来减少繁琐的重复工作,但在每个尺度上仍然有足够的”人在回路中“来审查和修复局部问题,以便让人类保持对所有尺度上任务结构的感知。
如果过度地在单一尺度上对AI进行基准测试,最终可能会对长期目标产生不利影响。
陶哲轩与ChatGPT合作史
而陶哲轩对AI辅助数学工作的可能性探索还要追溯到三年前——ChatGPT刚刚发布的时候。
陶哲轩在其诞生伊始就敏锐地察觉到它的作用,并就黎曼假设进行试探性询问,但得出的结果却让他大失所望:
ChatGPT给出了看似合理且相关的回答,但仔细检查后却没有任何实际的深度内容。

此时的ChatGPT还不能完全理解数学问题的本质,只是在将一些低质量内容进行包装掩盖,这意味着常规的表面检测方法不再准确,需要对核心内容进行人工筛查,例如逐行地阅读文本。
所以早期的陶哲轩对AI工具抱有怀疑审视的态度,认为AI在数学中的作用,是为答案提供近似值,然后人类数学家再通过传统方法进行逐步细化。
转机出现在GPT-4,陶哲轩尝试使用GPT-4协助处理统计数据,即把原始数据输入电子表格,并查找对应函数、计算所需内容。
短短几分钟,GPT-4就完成了人类一天的工作,期间只有非常少的部分需要校验,这也让陶哲轩开始期待将AI集成到软件工具中,尤其是处理90%以上的LaTeX编译问题。
我可以明确地说,今天是GPT4为我节省了大量繁琐工作的第一天。
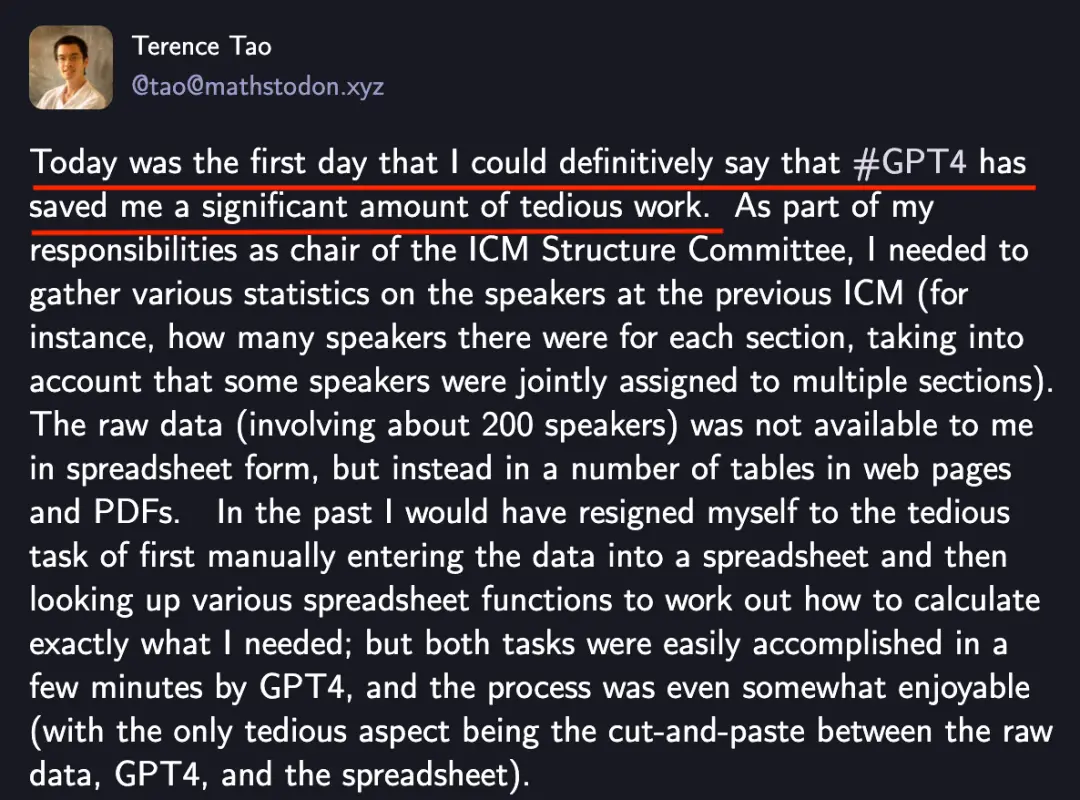
随后,他开始使用GPT-4处理一些自己熟悉领域的数学问题,比如下面这个问题:证明递归式(定义R)能够推导出a(n+1)。

GPT4从合作者的角度提出了八种不同方法,其中生成函数法引起了陶哲轩的注意,并随即沿着该解决路径,利用人工计算最终解决了这个问题。而最初陶哲轩想使用的是渐近分析方法,但事实证明AI可以更快地协助找到正确方案。
与此同时,他开始让ChatGPT编写Python来计算序列长度,虽然与预期的目标序列存在差异,只考虑到了连续整数的子序列而非任意子序列,但已经足够接近,而且其中在计算totient函数时还使用了非常独到的方案。
但代码本身有时也不够简洁、效率不高,或者逻辑不够严密,还是需要人工校正与重写。
他还尝试使用Copilot书写数学论文,不过在攥写证明大纲时,AI陷入了长篇叙述有关随机分析数论的废话,只有在编写非常短或重复的文本上有效。
所以此时的AI在陶哲轩看来,AI写数学论文仍然是有趣多过于有用。
在GPT-o1发布后,陶哲轩同样第一时间测试了其数学能力,显然相比于前代,GPT-o1的幻觉问题得到解决,在形式化任务中也作用显著,但在复杂分析问题上仍然令人失望,没有产生关键的概念思想。
陶哲轩将这一代模型定义为平庸但并非完全无能的数学“研究生”,而此前的模型则更接近为无能的“研究生”水平,不过他也相信再迭代一两次,加上与其他工具的集成,AI将在研究级别的任务中大有所为。

而今年七月份,OpenAI斩获IMO金牌一事让AI的数学能力再次引起热议,陶哲轩也对此做出了长文回应,认为缺乏统一的评测标准。
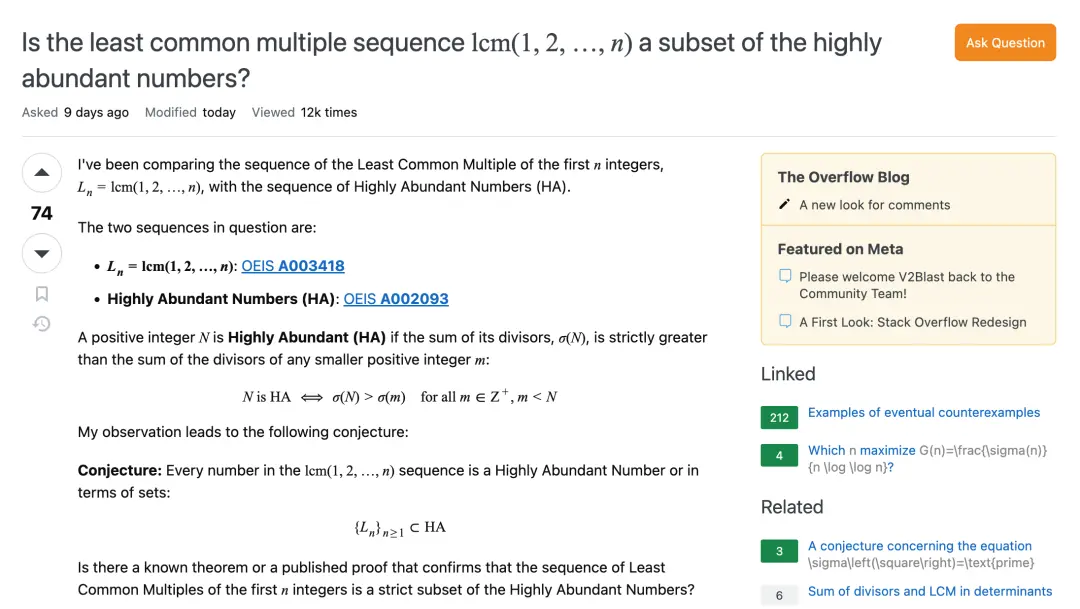
但同时他也开始让ChatGPT处理一些更为复杂的数学问题,比如在判断该集合是否是HA的子集时,陶哲轩通过理论分析已经确定该问题的答案是否定的,但仍需要一些数值参数来验证部分不等式。
起初,直接要求AI提供一个Python代码的反例,但由于初始参数问题始终失败,随后陶哲轩调整策略转而与AI逐步对话,使其执行启发式计算并找到可行的参数选择,通过单独验证生成的参数,最终解决了该问题。
陶哲轩总结认为,在数值搜索这类任务上,AI工具显然可以节省大量时间,如果没有AI,甚至他可能都不会考虑这种解决方法,而是寻求理论渐进分析。
而对于如何减少AI在数学问题中的幻觉或废话问题,陶哲轩也显然有了自己的一套心得,那就是在计算任务的每一步都做到详细解释,每一次和AI的对话都先确认再执行下一步,在对话结束后再使用Python进行外部验证,得到输出。
正如他一直所说的那样,AI正在重塑人类科学范式,其最合理的角色是成为数学家的“副驾驶”或助理,而不是取代人类在创造性、直觉性、策略性上的工作。
在AI的协助下,数学将在未来拥有更多的实验,而不仅仅是理论。
论文地址:https://mathstodon.xyz/@tao/115351400633010670
参考链接:
[1]https://chatgpt.com/share/68e85cba-7228-800e-8804-a0f41aa64e14
[2]https://mathoverflow.net/questions/425509/sphere-with-bounded-curvature
[3]https://terrytao.wordpress.com/mastodon-posts/

